M1.1 Aritmetika
Tedy:




















11



1,1




706,9






Velká čísla členěná v černotisku mezerou nebo tečkou se člení jen tečkou nebo se nečlení vůbec. Mezera se použít nesmí:
37.803







1299 327 305












2 736,5







Platnost číselného znaku je ukončen mezerou nebo libovolným znakem kromě tečky, čárky a písmen a až j.
Při zápisu výrazu s písmeny se postupuje shodně s černotiskem:
je-li mezi číslem a písmenem v černotisku mezera, zapíše se malé písmeno za mezerou, která ukončila platnost číselného znaku:
12 c





12 ab






5 x




není-li v černotisku mezi číslem a písmenem mezera, pak se písmen a až j zapíší bez mezery s prefixem malého písmene latinské abecedy, ostatní písmena k až z se zapíší bez mezery a bez prefixu:
12b





12k




34cd






34xy





pokud za číslem následuje velké písmeno latinské abecedy nebo řecké písmeno, zapisuje se písmeno s příslušným prefixem buď s mezerou nebo bez mezery podle černotiskové předlohy
7R




36 W





2πr





4 α





Řada čísel
– zapisuje se ve shodě s černotiskem při dodržování všech základních pravidel pro zápis, tj. každé číslo se zapisuje s číselným znakem a mezi nimi je vždy čárka a mezera:6, 9, 12 dělte ...





















.
krát
(též skalární součin vektorů)

×
krát
(vektorový a kartézský součin)

*
hvězdička, krát

:
děleno

|
dělí

±
plus nebo minus


Před těmito znaky se zapisuje mezera, za nimi nikoliv:
4 + 2






7 - 3






5.6






5.bc






28 : 4







M1.1.3 Zápis základních početních výkonů
(písemné sčítání, odčítání, násobení a dělení)
18
29
----
79



















1926
-------
5351























-29
----
14















-929
---------
2.903



























×25
-------
970
388
-------
4850











































.25
------















Zapisují-li se při písemném násobení oba činitelé vedle sebe, pak každý z nich musí být s číselným znakem. Další postup je shodný s již popsaným písemným násobením. S číselným znakem bude zapsán až výsledek:
-------------
388
970
-------------
4850

































































Písemné násobení
– postupuje se obdobně jako při násobení celých čísel pod sebou, tj. zapíše se první činitel s číselným znakem, pod něj se zapíše operační znak a druhý činitel bez číselného znaku a místo podtržení se vynechá řádek. Jednotlivé součiny se zapíší pod sebe, oddělí se volným řádkem a jejich součet se zapíše bez číselného znaku. Po určení počtu desetinných míst v součinu se výsledek zapíše s číselným znakem pod mezisoučet:.5,2
---------
2 4 6
6 1 5
-----------
6 3 9 6
63,96























































114
6












































Při dělení desetinného místa číslem celým se zapíše opět dělenec, dělitel i podíl s číselným znakem. Postupné zbytky se zapisují bez číselných znaků, ale na rozdíl od černotisku se zapisují s desetinou čárkou. Je-li ve zbytku desetinná čárka zapisována, odstraní se problémy s připisováním dalších číslic, které by měly být ve sloupcích pod sebou a bez problému se určí řád zbytku. Metodicky zcela jistě bude bez problémů zvládnout, že zbytek 2,3 jsou 23 desetiny a při dalším dělení se tedy dělitelem dělí číslo 23:
2,3
1,18
0,10















































































V případě, že dělenec i dělitel jsou desetinná čísla, postupuje se stejně jako v černotisku – po rozšíření se příklad přepíše na nový řádek a pak se postupuje jako v předchozích případech. Řád zbytku se pak upraví podle původního zadání:
26,38 : 12 = 2,19
2,3
1,18
0,10
zb.: 0,1 . 0,1 = 0,01



































































































































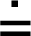
rovná se přibližně
(po zaokrouhlení)


>
větší než

<
menší než

≥
větší nebo rovno


≤
menší nebo rovno


<>
menší nebo větší než


Před těmito znaky se důsledně zapisuje mezera, za nimi nikoliv:
6 + 4 = 10











x = 6 . 7









a + x = 50









3 . x = 21














a < b




y ≠ 2






1 < z < 12










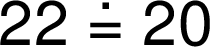









Pokud za znakem rovnosti či nerovnosti následuje záporné číslo, nezapisuje se ani před znakem minus mezera:
a = -7






-5 < -3








M1.1.5 Zlomky
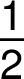
zlomková čára

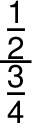
hlavní zlomková čára


znak začátku zlomku

znak konce zlomku

desetinná čárka

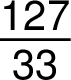










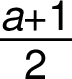










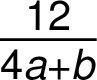













Zápis matematických operací se zlomky se neliší od zápisu těchto operací s celými čísly:
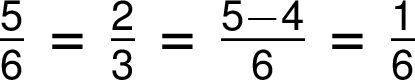








































Při zápisu delšího matematického výrazu se ukončí zápis na řádce operačním čí relačním znakem, který se na začátku nové řádky zopakuje.
V případě, že čitatel i jmenovatel zlomku jsou celá kladná čísla, připouští se v běžném textu zjednodušený zápis: zapíše se čitatel s číselným znakem a bez zlomkové čáry se zapíše jmenovatel „sníženou číslicí“ (odpovídající bodová kombinace se místo do prvního a druhého řádku znaku zapíše do druhého a třetího řádku znaku):
1/2 kg






5/3 l





V matematice se tento zápis nedoporučuje.
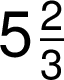









Případně v textu:





Jestliže čitatel nebo jmenovatel je číslo záporné nebo desetinné, zapisuje se zlomek důsledně podle základních pravidel:
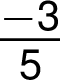








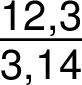













Složený zlomek se zapisuje podle stejných pravidel jako zlomek jednoduchý, označí se tedy jeho začátek znakem „začátek zlomku“, hlavní zlomková čára se zapíše zdvojenou zlomkovou čárou a konec zlomku se označí znakem „konec zlomku“. Pro zápis zlomků v čitateli nebo jmenovateli platí nezměněná pravidla.
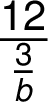













![]()














Dobrým vodítkem pro orientaci v zápisech složených zlomků je skutečnost, že složený zlomek má zdvojené buď oba znaky začátku nebo konce zlomku, nebo alespoň jeden z nich.
27,44






0,02





![]()






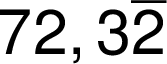








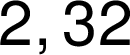








M1.1.7 Poměry
Poměry se zapisují ve shodě s černotiskem jako dělení:
3:5






a:b




Stejným způsobem se zapisují i úměry:
y : 3 = t : 9













Jsou-li jednotlivé členy poměru či úměry zapisovány kombinací číslic a písmen, pak zapisujeme písmena a až j a prefixem malého písmene, ostatní bez mezery:
3c : 5y









2z:3 = 12:9
















%
procento


‰
promile


Před značkou procenta a promile se nikdy nepíše mezera:
50 %





7,5 %






p %



12 ‰





9 % ze 700












M1.1.9 Závorky
(
závorka levá

)
závorka pravá

[
hranatá závorka levá


]
hranatá závorka pravá


{
složená závorka levá


}
složená závorka pravá


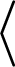
úhlová závorka levá (interval)


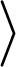
úhlová závorka pravá (interval)



absolutní hodnota, svislá čárka

Výraz v závorce se od znaků závorek neodděluje mezerami:
(2 + c)







Začíná-li výraz v závorce znakem mínus, nepíše se před ním mezera:
(-3 + 2)


















Pro zápis množiny výčtem prvků se užívá složené závorky:
K = {-1, 0 , 1}



















Ve shodě s černotiskem se nevypisuje znaménko násobení mezi číslem a závorkou ani mezi dvěma závorkami:
5(3+c)









(a+b) (a-b)












3[2 + (-x + 5)]


















indexy zapisované v černotisku vpravo nahoře či vpravo dole za znakem se zapisují bezprostředně za znakem, k němuž přísluší. Zápis indexu se ukončuje znakem konec indexu:
ta




vb




Číselné indexy se zapisují vždy s číselným znakem:
M1






k2





Zápis matematických operací se provádí stejně jako u znaků bez indexu:
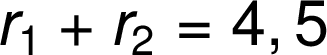


















![]()





















znak exponentu
(index vpravo nahoře)

znak odmocnitele
(index přesně shora)


odmocnítko √

závěr výrazu daného typu

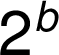





![]()





Je-li v exponentu číslo, zapisuje se důsledně s číselným znakem:
![]()






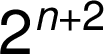









Znak závěru exponentu lze vypustit v případech, kdy není zpochybněna jednoznačnost zápisu. Jedná se o zápis mocniny v jednotkách obsahu a objemu, před relačními znaky, množinovými symboly a pod.:
![]()









![]()











![]()








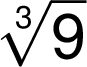








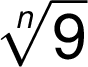







Při zápisu druhé odmocniny je možné použít jak plného, tak i zkráceného zápisu – ve shodě s černotiskem – bez odmocnitele:
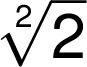








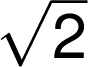




Matematické operace s odmocninami se zapisují stejně jako operace s čísly a k vyznačení součinu se ve shodě s černotiskem nemusí zapsat znak násobení:
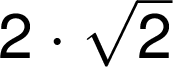







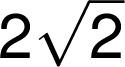






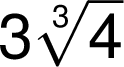










Tam, kde není zpochybněna jednoznačnost zápisu, připouští se zjednodušený zápis: index odmocniny se zapíše jako index vpravo nahoře. Zjednodušeného zápisu lze použít, předchází-li mu mezera, relační nebo operační znak a pod.:
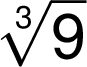








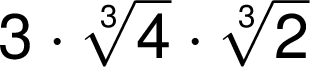




















![]()


































Pokud se zápis výrazu nebo výpočtu nevejde na jeden řádek, rozdělí se v místě operačního nebo relačního znaku, který se na začátku nové řádky zopakuje.
M1.1.12 Množinová symbolika
je prvkem, náleží
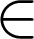


není prvkem, nenáleží
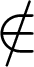



je podmnožinou



není podmnožinou
![]()



je nadmnožinou



sjednocení
![]()


průnik
![]()


prázdná množina



nekonečno
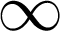


Zápis množiny výčtem prvků je shodný s černotiskem:
M = {0, 1 , 2}


















Před i za znakem množinové symboliky se vždy píše mezera:
![]()







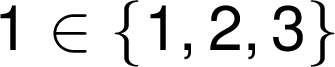




















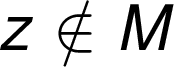








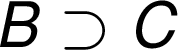








![]()












Následuje-li po indexu vpravo dole znak množinové symboliky, není nutné vyznačovat konec indexu:
![]()












![]()













![]()


















Zápis průniku množin užíváme v souladu s černotiskem i při zápisu rozboru a konstrukce v geometrii:
![]()


















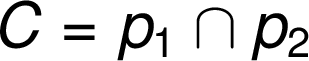
















![]()







M1.1.13 Vektory
vektorová šipka


Vektory zapisujeme zkráceně tak, že za značku vektoru zapíšeme bez mezery vektorovou šipku:
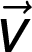



Vektor lze pro přesnost přepisu z černotisku zapsat s použitím značky pro index přesně shora:
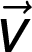





Při běžném psaní se však užívá zkrácený zápis:
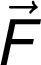




V tisku lze vektor vyznačit shodně s černotiskem tučně:





Goniometrické funkce zapisujeme důsledně v souladu s černotiskem:
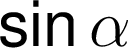



















![]()







Matematické operace s goniometrickými funkcemi se zapisují ve shodě s černotiskem podle všech obecně platných pravidel:









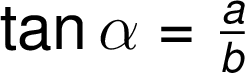












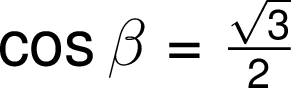

















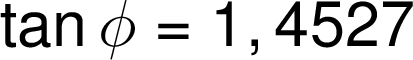















 Z.7 Základní pravidla pro přepis běžných textů do bodového písma
Z.7 Základní pravidla pro přepis běžných textů do bodového písma
 Z Základní pravidla pro přepis běžných textů do bodového písma: obsah
Z Základní pravidla pro přepis běžných textů do bodového písma: obsah
 M1 Přepis matematických textů pro ZŠ do bodového písma: obsah
M1 Přepis matematických textů pro ZŠ do bodového písma: obsah
