Dijkstrův algoritmus
1. Popis standardní metody algoritmu
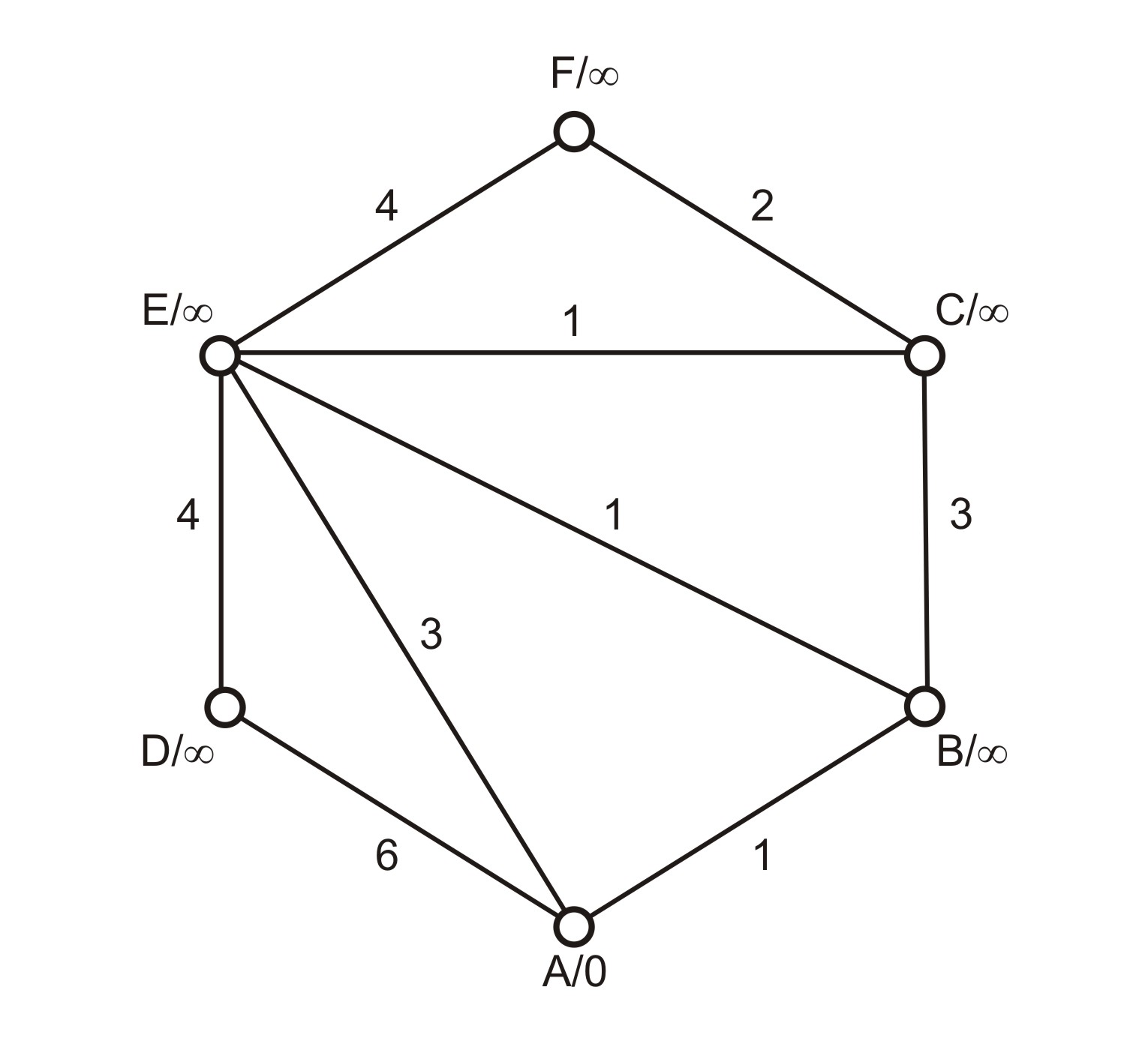
Dijkstrův algoritmus slouží k vyhledání nejkratší cesty z iniciálního uzlu $A$ do všech ostatních uzlů grafu. Pracujeme s váženým neorientovaným grafem $G = (V, E, w)$, kde $V$ je množina vrcholů, $E$ je množina neorientovaných hran a $w$ je ohodnocení hran. Na počátku algoritmu vložíme do návěští iniciálního uzlu $A$ hodnotu "$A/0$", do návěští ostatních uzlů $X$, jejichž vzdálenost od $A$ zatím neznáme, zapíšeme "$X/\infty$". Ukázku takového grafu nabízíme na Obrázku 1.
Příklad 1: Neorientovaný graf $G$
Opakovaně provádíme následující tři kroky, dokud nezpracujeme všechny vrcholy:
- Mezi nezpracovanými vrcholy najdeme uzel "$X/n$" s nejmenší vzdáleností $n$ od iniciálního $V$.
- Pro každou hranu $e$ vedoucí z uzlu "$X/n$"
do nezpracovaného vrcholu "$Y/m$" provedeme následující:
- je-li $m > n + w(e)$, změníme aktuální vzdálenost uzlu $Y$ od iniciálního uzlu na $m = n + w(e)$,
- v opačném případě ponecháme návěští uzlu $Y$ beze změny.
- Označíme uzel $X$ jako zpracovaný.
Při aplikaci Dijkstrova algoritmu měníme pouze návěští vrcholů. Aktualizujeme jejich aktuální vzdálenost od iniciálního uzlu, nebo je označujeme za zpracované. Pro názornost uvádíme i konkrétní příklad neorientovaného grafu a Animaci 1 naznačující výpočet nejkratších vzdáleností od iniciálního uzlu pomocí Dijkstrova algoritmu.
2. Návrh možných adaptací
1. Práce s grafem v jednom listu tabulkového procesoru:
Do prvního sloupce zapisujeme návěští jednotlivých uzlů počínaje iniciálním uzlem. Do dalších buněk na stejném řádku pro uzel $X$ zapisujeme všechny hrany z něj vycházející, a to ve formátu $n$–$Y$, kde $n$ je ohodnocení hrany, $Y$ je koncový uzel hrany, viz Tabulka 1.
Příklad 1: Neorientovaný graf $G$ z Obrázku 1
| $A/0$ | $1$–$B$ | $3$–$E$ | $6$–$D$ | ||
| $B/\infty$ | $1$–$A$ | $1$–$E$ | $3$–$C$ | ||
| $C/\infty$ | $1$–$E$ | $2$–$F$ | $3$–$B$ | ||
| $D/\infty$ | $4$–$E$ | $6$–$A$ | |||
| $E/\infty$ | $1$–$B$ | $1$–$C$ | $3$–$A$ | $4$–$D$ | $4$–$F$ |
| $F/\infty$ | $2$–$C$ | $4$–$E$ |
Editujeme pouze návěští uzlů v 1. sloupci, hodnoty v ostatních sloupcích slouží pouze pro čtení. Zpracovaný uzel označujeme hvězdičkou, abychom jej při dalším pokračování algoritmu nemuseli brát v potaz. Algoritmus končí, jakmile máme všechny uzly označené hvězdičkou (jsou tedy všechny zpracované).
2. Práce s grafem ve dvou listech tabulkového procesoru:
Oproti předchozí metodě dochází k jediné změně. 1. list používáme pouze pro čtení hran, na 2. listu máme pouze sloupec s návěštími uzlů, které postupně upravujeme.
3. Práce s grafem ve formě hmatového obrázku, zápis vzdáleností uzlů v libovolném editoru:
Metoda je podobná předchozímu postupu s tím rozdílem, že graf je nabízen v podobě hmatového obrázku. Student tak kombinuje čtení hmatem s editací návěští jednotlivých uzlů zapsaných v libovolném textovém či tabulkovém editoru.
3. Diskuze nad výhodami a nevýhodami
Je patrné, že první navržená metoda je výhodná pro učitele co se týče přehlednosti. Reprezentaci grafu má na jednom místě a je celkem srozumitelná. Z hodnocení nevidomých studentů vyplývá, že není efektivní vzhledem k poměrně častému pohybu mezi jednotlivými řádky a sloupci jednoho listu tabulky.
Tuto nevýhodu smazává druhá metoda. Při pohybu mezi oběma listy zůstává kurzor na místě, kde byl naposledy, tudíž zpracovávaná data má uživatel ihned k dispozici a nemusí je na listu zdlouhavě hledat. Navíc klade menší paměťové nároky. Při přepínání mezi listy si student potřebuje zapamatovat pouze nejkratší vzdálenost aktuálně zpracovávaného uzlu, ostatní údaje jsou snadno a rychle dosažitelné. Jednoho ze studentů dokonce napadlo zajímavé vylepšení: "Informace o aktuálně zpracovávaném vrcholu bych si mohl zapisovat třeba do názvu listu. Tyto informace jsou trvale k dispozici na braillském řádku, kdykoliv mám list otevřený, takže si je nemusím pamatovat."
Třetí metoda respektuje rovinné uspořádání grafu, které používají vidomí uživatelé algoritmu. Nevidomými studenty byla hodnocena nejlépe. "Mně přijde lepší pracovat s grafem v hmatové podobě. Člověk si udělá lepší představu o vztazích mezi uzly. V tabulce jsou vrcholy pod sebou uspořádané podle abecedy, přesto vůbec nemusí být sousedy," řekl jeden z nevidomých studentů Masarykovy univerzity. Zkušenější nevidomí uživatelé doporučili zapisovat všechny uzly grafu na jednom řádku textového editoru a neoddělovat je, jeden po jednom, na samostatné řádky, jak jsme původně navrhovali. Jelikož používají hmatový displej, mohou totiž okamžitě prozkoumat veškeré (ne)navštívené vrcholy bez pohybu kurzorem.